【中学受験④】応用問題を解かないとつかない力がある。【難関校の合否を分けるもの】

こんばんは～！

つつです。

続きです。

www.tutukun.com

基礎問題の重要性

 前の記事ではちょっと言い過ぎました。

基礎問題は重要です。

やらなくて良いとは言ってはいません。

基礎は１００％完璧にする必要は無い。

約６～7割やれば良いといいたいだけです。

・・・・

残り3～4割の基礎は応用問題を解き続ければ自然と上がります。

逆に、

応用問題を解くときに基礎部分が出てくるとより強く印象に残ります。

応用問題を解いていると

「あぁ！この基礎問題はこういう所で使うんだ！」

そういう経験をたくさん積む事ができます。

簡単な基礎問題で１００点を取って自信をつけることも大事ですが、応用問題には別の良さがあります。

そういった基礎を発展させた問題は、よい問題だと私は思います。

沢山の応用問題に触れることで多くの気づきが得られ、頭を良くする効率的な方法だと思います。

知らないと解けない図形問題が出る。

話は大分変わります。

難関私立中学校である、

某学園の入試問題です。

2021年の問題です。 

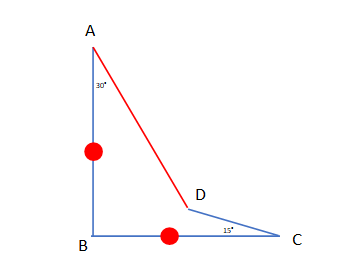
辺ABと辺BCは同じ長さです。

∠BAD30°　∠BCD＝15°　　∠ABC＝直角

この時、辺ABとADの比を求めよ。　

この問題はぱっと出来ないとダメです。

ぱっと見、ABとBDは1対1に見えます。

しかし・・・

難関校の問題はそんな簡単な数値になる事は稀です。

１  対　23/21

みたいに、割り切れない分数になることもよくあります。

だから難関校の難しいのです。

あてずっぽうで答えてもマズ正解しません。

答えはこの下へスクロール！！！

たぶん、考える人はあまり居ないと思うので、早速解答をのせます。

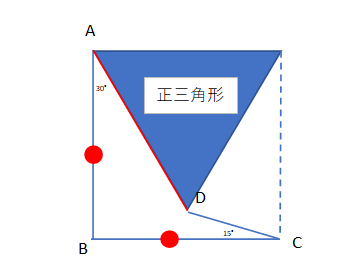
この図形は、丁度この部分に正三角形が入って全体で正方形になります。

よって、辺ABと辺ADの比率は１対１です。

・・・

ええ！

いちたいいちです。

正三角形と正四角形をこのように配置した場合、∠BCDは１５°になる。

と知っているか否かです。

ちなみに∠DBCは75°ね。

もし知らなくても頑張れば解けるのかもしれませんが、とても時間がかかります。

上の知識があれ5秒で解けます。

超サービス問題です。

私も頑張って考えてみて、塾の先生にも質問しましたが簡単に証明する事は難しそうです。

1対1を入れてみて計算すると矛盾がないことが分かるのでそれでいいのか・・・？

この差は大きいです。

もし、この問題に時間をかけてしまったら。

残念ながらその時点で既に不合格です。

知らなかったら終わりです。

知らなくても、適当に１対１と書いて次の問題に取りかかったら合格する可能性は飛躍的にあがります。

この問題は、応用問題を沢山といて知識を持っていないと解けません。

正三角形と正四角形をこのように配置した場合、∠BCDは１５°になる。

この知識を持っているかどうかです。

塾の通常授業では出てこないと思います。

出る塾もあるのかな・・・

実際に難関校の過去問を解いていると、そういった知らないと解けない問題も沢山あります。

応用問題を解くことでつく力

応用問題を解くことでつく力は、他にもあります。

例えば、計算の正確性とスピードです。

計算の正確性とスピードをあげるにはソロバンとか計算問題を沢山やることが一番じゃない？と思うかもしれませんがそうでもありません。

計算問題の正確性とスピードを上げるために計算練習をさせても、なかなか早くなりません。

理由は、子供自身が本当に心の底から

計算問題の正確性とスピードをあげたいとは思っていないからです。

応用問題に頑張ってチャレンジして、せっかく解法が分かったのに、最後の計算でミスをしてしまい点を取れなかった。

時間が足りずに分かったはずの問題を落してしまった。

そんな悔しい経験をする事で、初めて子供自身が計算の正確性とスピードの重要性を理解するのです。

すると、計算練習にも気が入って「計算の正確性とスピード」が上がるのです。

ただ単純にうちの子はソロバンを習わせてるから計算は得意なはず！なんて考えていても思ったような効果はあがらないのです。

※実際にきゅーたろうにソロバンを習わせましたが、どこまで効果があったか疑問です。

難関校の合否をわけるもの

難関校に合格する生徒の全てが天才な訳ではありません。

どれだけ応用問題にチャレンジしたかです。

で子が思いますに、

知ってるかどうか･･････と言うか、この問題については図形について突き詰めて考えた経験の多さをさぐられている気がします。整数問題も、数の性質について考え抜いた経験の多さを試されてるよね。

↓例えばこういうコトしたことありますか？

【算数】折り紙で正三角形を作るには？

↓ついでに、お勧めの本↓

おりがみで学ぶ図形パズル 小学校全学年用算数 [ 山口 榮一 ]

こういった、問題を沢山こなせばこなすほど

知識が増えて、

知らない問題が減って、

知ってる問題が増えて、知識がつながって

初見問題の糸口に気づきやすくなって、

合格する確率があがります。

どうすれば、沢山の応用問題に出会うことができるか。

やはり塾へ行くことです。

普通の親には、最難関校中学受験向けの問題を教える事は不可能です。

上の問題を５秒で解けましたか？

ただ難問の問題集を買ってきてポン！と渡せばオッケーという物ではありません。

 特に早くから難問に取組もうと思ったら、持っている知識で解ける問題かどうかを選別する必要があります。

そこに「塾のノウハウ」があります。

塾の中でも出来る限り上のクラスに入る事に大きな意味があります。

上のクラスにいればいるほど、沢山の応用問題を与えられます。

周りの出来る子から受ける刺激も全然違います。

せっかく中学受験するんだから、

出来る限り背伸びをして手を伸ばして届く、ギリギリ一番上を目指すのが楽しい！ってものじゃないかな。

すると、子供達は大人が思うよりもドンドン成長して、思ったよりもアッサリと志望校に合格する！

と思いますよ。

じぃ～かい　効率中受！！

絶対に知っていないと無理だと思われていた、

某大和学園の入試問題に「つつ」が挑む！

はたして！

納得するゴールにたどり着くことができるのか！！！

相手にとって不足なし！

俺（効率厨）の歴史にまた1ページ！

解けなかったらカンベンな！