こんばんは~!
つつです。
この記事の続きですよ。
頑張って問題を解いてみました。
中学受験生はこんな難しい問題を解いているのですね・・・
他のサイトやYouTube動画動画よりも、もう少し納得のいく解答にたどり着いたと思います。
図形問題の基本
中学入試に出てくる図形問題の解法は基本的に2つのパターンがあります。
1、2等辺三角形をみつける。(補助線を引いて作る)
2、正三角形をみつける。(補助線を引いて作る)
大体この2つで解けます。
立体になっていたりしますが、平面に展開して結局はこの2つです。
60°を見つけたら正三角形です。
足したり引いたりして同じ角度になる2角を見つけたら2等辺三角形です。
問題!
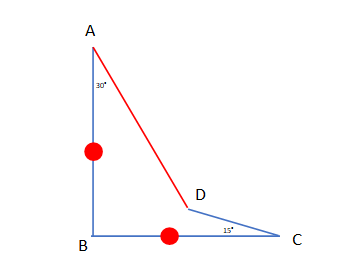
辺ABと辺BCは同じ長さです。
∠BAD30° ∠BCD=15° ∠ABC=直角
この時、辺ABとADの比を求めよ。
直ぐ下に解答があるので、チャレンジしたい人は解いてみてね。
この問題の解法を見て
もちろん、最初は解法を見ずに考えましたが無理でした。
なので他サイトやYouTube動画から解法を探しました。
その結果がコレです。
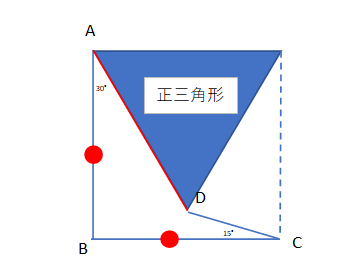
丁度ピッタリこの形に正三角形が入って、全体で正方形になるので
AB対AD=1対1
となる。
秒殺です。
この解法で納得出来ますか?
この解法だと
正三角形と正方形をこのように並べた場合、∠BCDが15°になる。
このことを知っていないと解けません。
それって、図形問題としての美しさは無い気がします。
・・・・とけた!
頑張ったら解けました。
私には2日かかりました。
最初にも述べましたが
正三角形を無理矢理つくる。
2等辺三角形を無理矢理作る。
コレが図形問題の基本です。
最初の図形
AB対ADの比率を求めよ!

1、点Aから横に水平に線を引く

出来た∠Aは60°と分かる。
∠ADCは135°ね。
2、∠Dから60°の線を延ばし、正三角形をつくる。

残った∠CDEは75°ね。
交点は点Eとする。
3、点Cから垂線をのばす。

∠DCEは75°なので△CDEは2等辺三角形とわかる。
∠CEDは30°とわかる。
点Eで60°+30°=90°となり1点になる。
なので、□ABCEは正方形になる。
△ADEは辺AEを共有した正三角形なので
辺ABと辺ADはいちたいいち!
納得!?
おお!
「正三角形と正方形をこのように並べた場合、∠BCDが15°になる。」
この知識が無くても問題を解くことが出来ました。
答えから逆算しているような気もしますが、まぁ良しとしましょう。
悩んだ分だけ賢くなる。
色々な問題に出会って悩んだ分だけ賢くなります。
答えを見たら終わりではありません。
難問は答えを見てもピンと来ないことが良くあります。
自分が納得する解法にたどり着くまで考える事が重要だとおもいますよ。
これで私も大分賢くなったかな!
つつお。
西大和学園2021年入試問題の⬜3(3)の詳しい解説をのせるよ!
— つつ@効率厨の考えた最強の中学受験!ブログ (@tutu_kouritutyu) 2021年2月1日
解くのに2日もかかったよ!(笑
西大和学園2021年入試問題大問3(3)図形問題の基本的な考え方 - 効率厨(オレ)の考えた最強の中学受験ブログhttps://t.co/dM8J6HKafu









